Solar

Sampling Procedures for Inspection and Sampling Plans for Lot Inspection Using ISO 2859

Sampling is a technique in which samples are drawn at random (without any favor or bias). For this, suitable measures or procedures may be laid down and adopted according to the nature and configuration of parts under inspection for ensuring complete randomness in sample selection. The term sample implies a subset chosen from the population.

Acceptance sampling is an important method used in sampling procedures. It is also an important field of standard quality control where a random sample is taken from a lot, and upon the results of appraising the sample, the lot will be either rejected or accepted. It is also a procedure for inspecting quality of batches without doing 100% inspection. So, acceptance sampling is also known as the “middle-of-the-road approach” between no inspection and 100% inspection. The cost associated with 100% inspection is often prohibitive, and the risks associated with lesser or 0% inspection are very large.

Acceptance Sampling by Attributes. Evaluations using attributes are generally based on “go” and “no-go” gauge inspections. A sample is taken and if it contains too many non-conforming items then the entire batch is rejected, otherwise, the batch is accepted.

Acceptance Sampling by Variables. Evaluations using variables may also be known as continuous measurement. The decision rule for selection and rejection of a lot in this type of sampling depends on a statistical tool, such as mean and standard deviation.

A decision on whether to use Acceptance Sampling by Attributes or Acceptance Sampling by Variables will depend on the particular circumstances of each case. However, it is noteworthy to mention that ISO 2859 deals with Acceptance Sampling by Attributes only.

Types of Sampling Plans

The most important element of acceptance sampling is choosing an appropriate sampling plan, which specifies the lot size, sampling size, number of samples, and acceptance/rejection criteria. Hence, considering all these parameters, acceptance sampling is typically of three types: single, double, or multiple sampling plans.

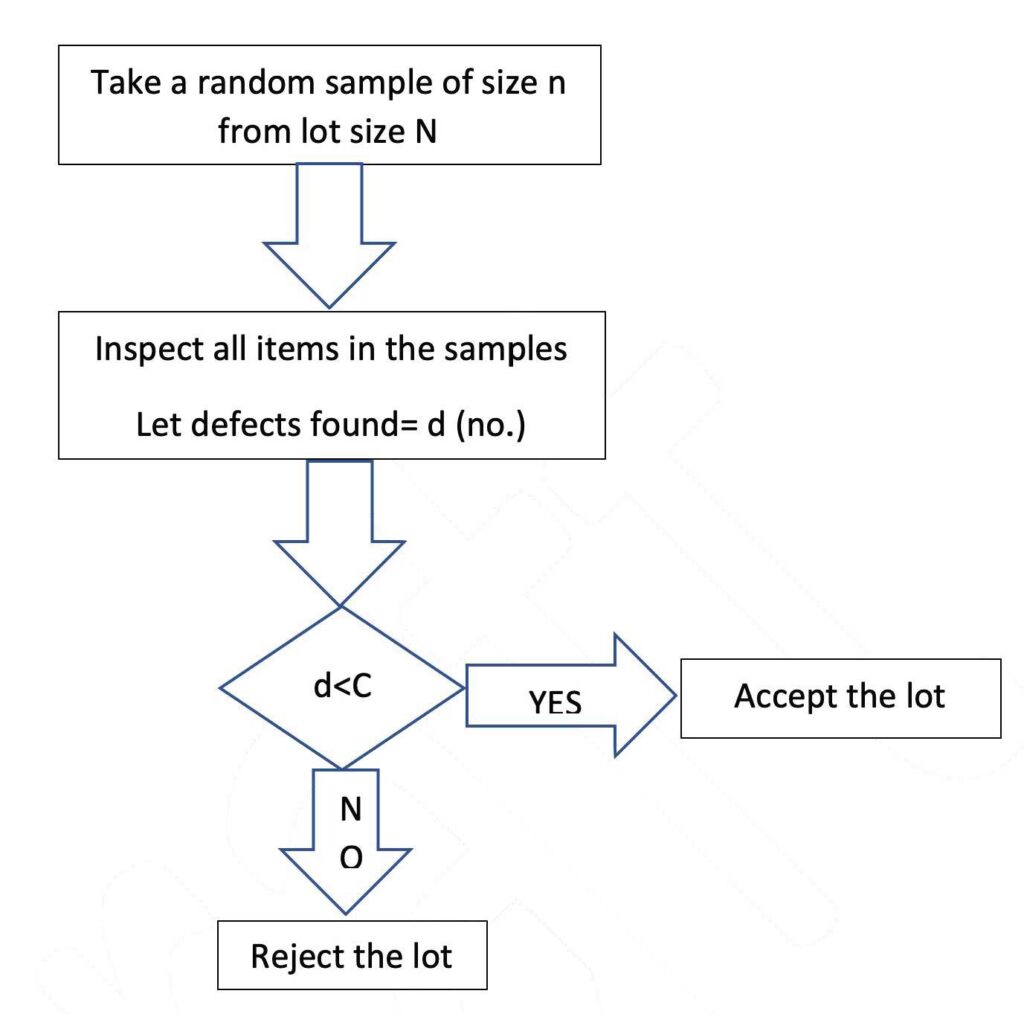
Single Sampling Plan. In this type of sampling plan, the decision for acceptance or rejection of the lot is made on the basis of only one sample. The acceptance plan is known as a single sampling plan. It generally follows the flowchart in Figure 1.

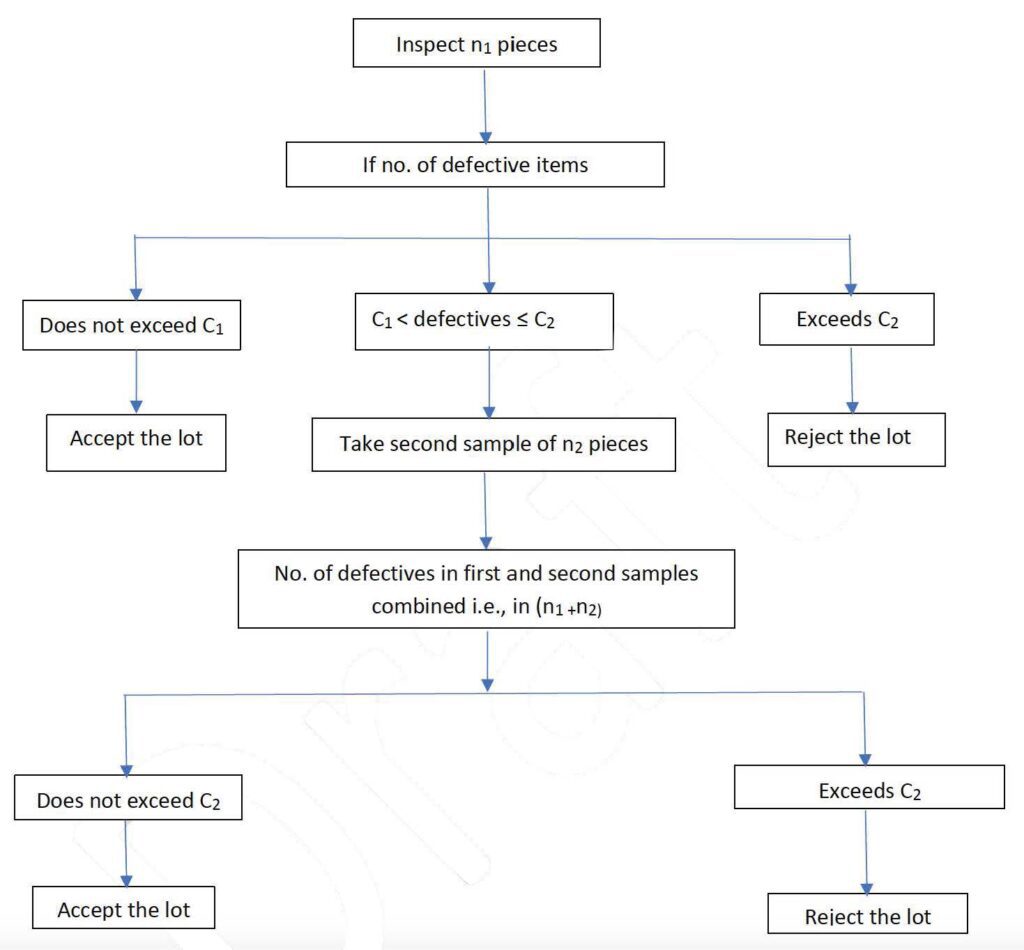
1. Let N = lot size, n = sample size, C = acceptance number, and d = the number of defective items in the sample. The standard rule would be: if d < C, accept the lot, but if d ≥ C, reject the lot. Courtesy: Mahindra Teqo Pvt. Ltd.

Double Sampling Plan. In this type of sampling plan, the decision on acceptance or rejection of the lot is based on two samples. It generally follows the flowchart in Figure 2.

2. Let N = lot size, n1 = number of pieces in first sample, C1 = acceptance number for first sample, d1 = number of defective items in the first sample, n2 = number of pieces in second sample, n1 + n2 = number of pieces in two samples combined, C2 = acceptance number for the two samples combined, and d2 = number of defective items in the two samples combined. The standard rule would be: if d1 ≤ C1, accept the lot; if d1 > C2, reject the lot; but if C1 < d1 ≤ C2, then evaluate the two samples combined. The rule in that case would be: if d2 ≤ C2, accept the lot, but if d2 > C2, reject the lot. Courtesy: Mahindra Teqo Pvt. Ltd.

Multiple Sampling Plan. In this plan, a decision to accept or reject the lot is taken after inspecting more than two samples. In this case, if the cumulative number of defective items in a sample is more than the upper limit specified for that particular sample, the sampling procedure is terminated and the lot is rejected. On the other hand, if the total number of defective items in a sample is less than or equal to the lower limit specified, then also sampling is terminated and the whole lot is passed.

Sampling Terms and Their Definitions

Several important terms apply to sampling procedures and plans. They include the following.

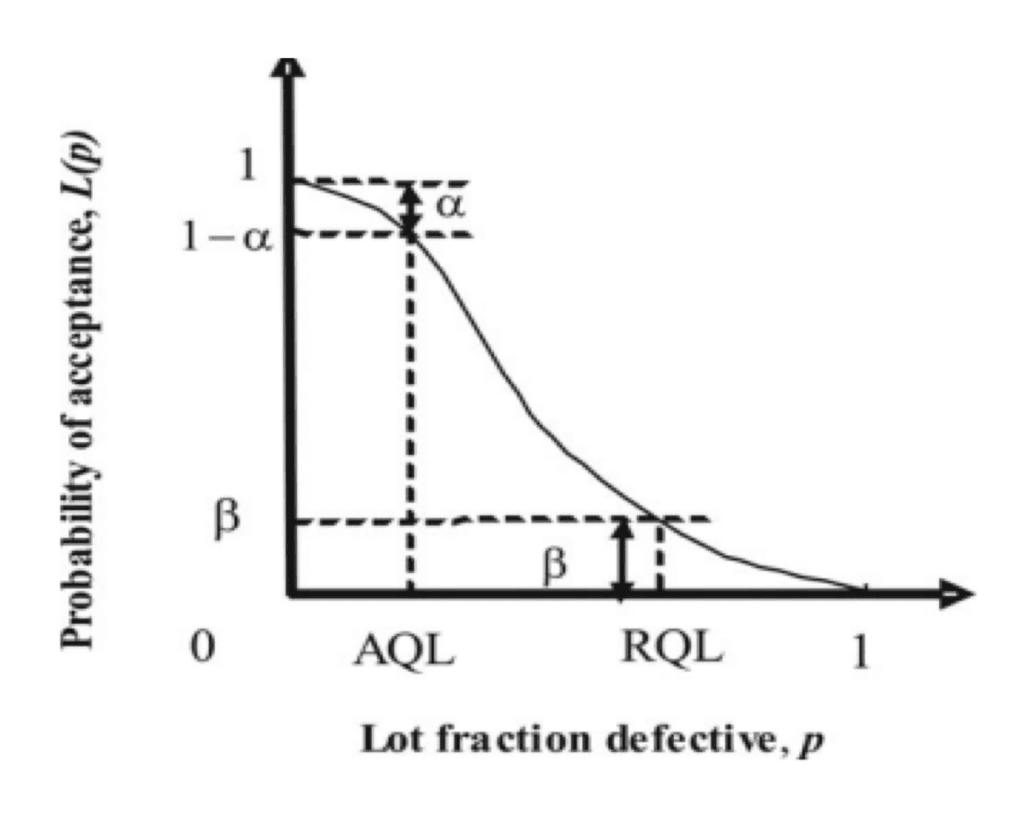
Acceptance Quality Limit (AQL). The AQL defines the percentage of defects at which consumers are willing to accept lots as “good.” The producers would like to design a sampling plan such that there is high probability of accepting a lot that has a defect level less than or equal to the AQL. In other words, the AQL is the worst tolerable quality level.

Lot Tolerance Percent Defective (LTPD) or Rejectable Quality Level (RQL). These terms define the upper limit on the percentage of defects that a consumer is willing to accept. In other words, it is the poorest level of quality that the consumer is willing to tolerate in an independent lot. The probability of accepting a lot of RQL represents a risk for the consumer.

Average Outgoing Quality (AOQ). AOQ represents the average percentage defectives in the outgoing products after inspection including all accepted and all rejected lots.

Producer’s Risk/Manufacturer’s Risk (α). α represents the probability that a lot containing AQL will be rejected.

Consumer’s Risk (β). β represents the probability that a lot containing defectives more than LTPD/RQL will be accepted.

Operating Characteristic Curve (OC Curve)

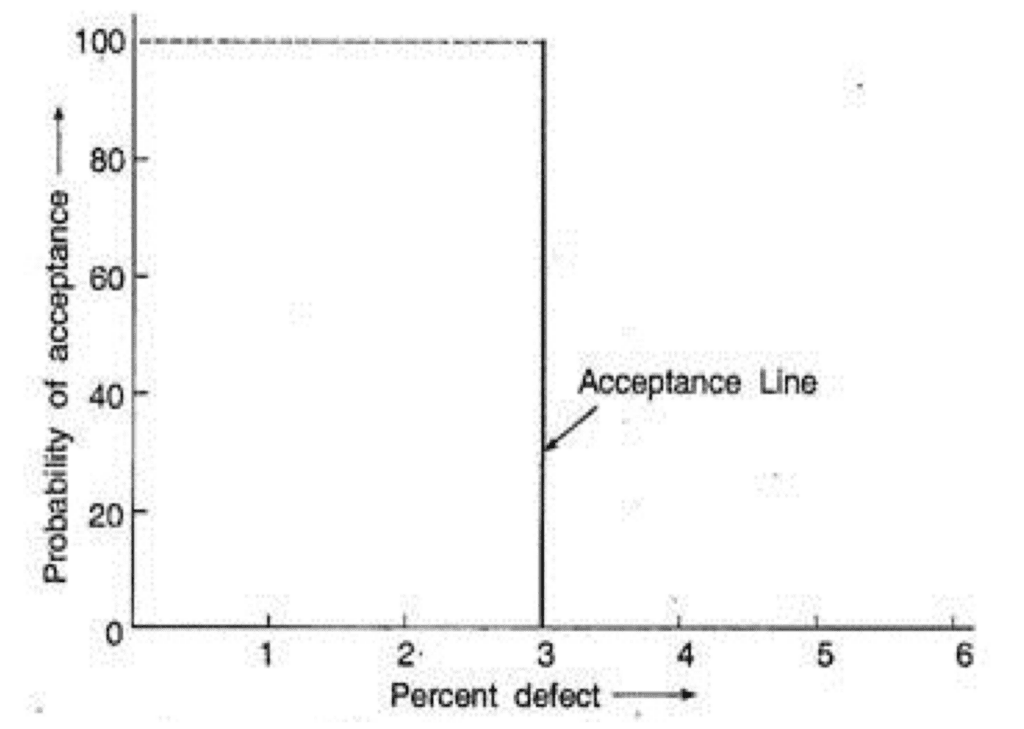
The OC curve is one of the major tools for representing and investigating the properties of a lot acceptance sampling plan. Figure 3 depicts an ideal curve. For the curve shown, all lots with less than 3% defects have a probability of acceptance of 100% while all lots with more than 3% defectives have a probability of acceptance as 0%. However, the sample size needed for such a plan is infinite. Hence, such a plan does not exist in reality. It may be noted that in this case, 3% is the worst tolerable quality level, that is, AQL.

*3. An Ideal Operating Characteristic Curve. Courtesy: Mahindra Teqo Pvt. Ltd.*

Let us consider a practical OC Curve (Figure 4). It shows probability of acceptance L(p) as a function of lot fraction defective (p). This curve is based on sampling plans. It aids in selection of plans that are effective in reducing risks.

Here, the probability of acceptance can be found using the equation:

L(p) = 1 – L(r)

where, L(r) = probability of rejection.

*4. A Practical Operating Characteristic Curve. Courtesy: Mahindra Teqo Pvt. Ltd.*

Lot Inspection Using ISO 2859-2:2020

As per ISO 2859-2:2020, “Sampling Procedures For Inspection By Attributes – Part 2: Sampling Plans Indexed By Limiting Quality (LQ) For Isolated Lot Inspection,” the sampling plan is indexed by a series of specified values of LQ, where β is less than 10%, except under some circumstances. This standard is valid both for inspection of non-conforming items as well as for inspection of non-conformities per 100 items. It is intended to be used when both supplier and consumer regard the lot to be in isolation. This means that the lot is unique in the sense that only one of its types is produced.

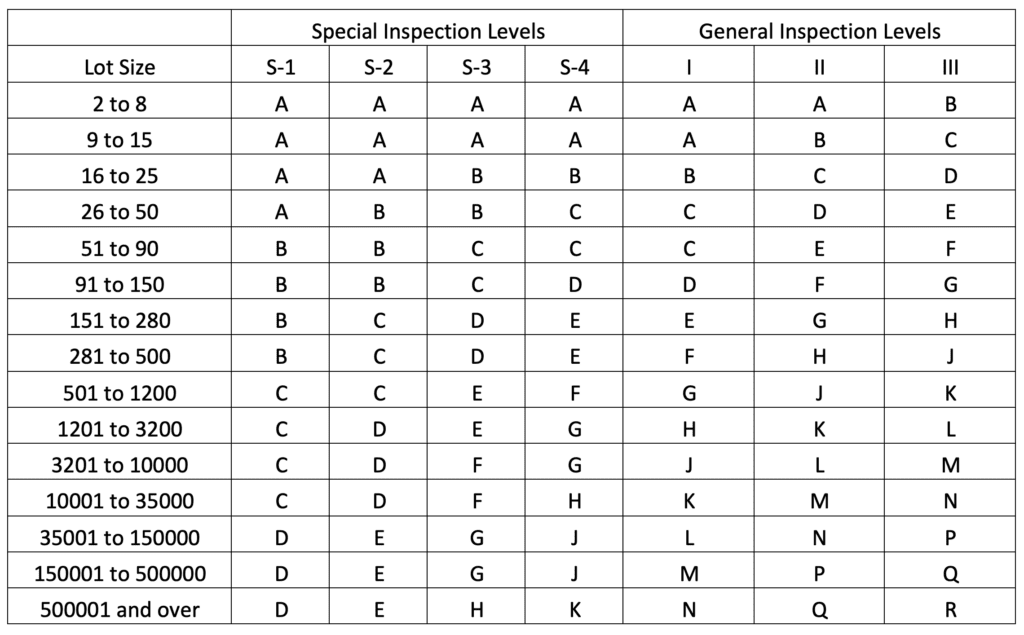
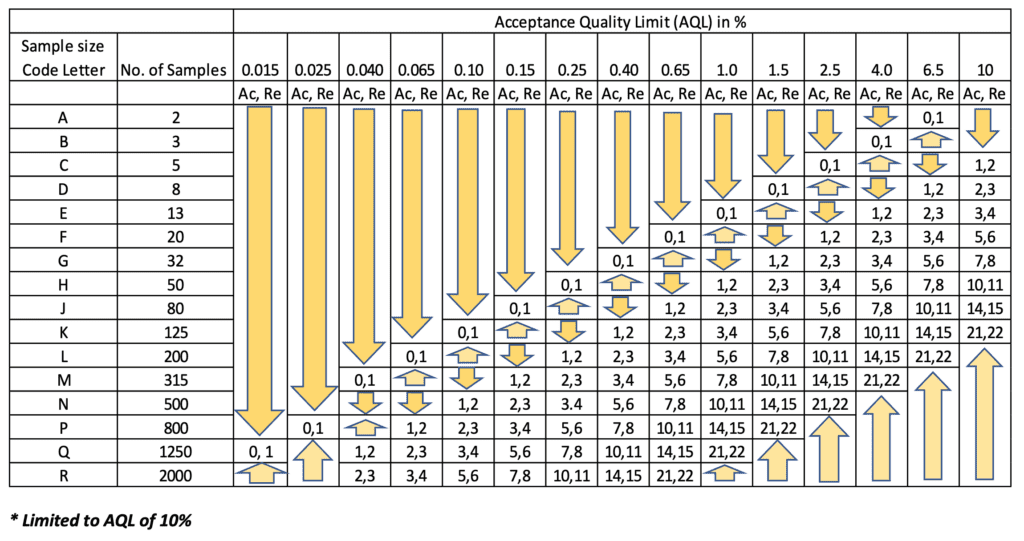
Tables 1 and 2 are useful in choosing the appropriate sample size corresponding to a fixed AQL for a particular lot inspection.

*Table 1. Sample size code letter selection. Courtesy: Mahindra Teqo Pvt. Ltd.*

*Table 2. Single sampling plan for normal inspection. (Master table limited to AQL of 10%.) Courtesy: Mahindra Teqo Pvt. Ltd.*

The steps to follow while selecting a sampling plan include:

Decide AQL and choice of sampling plan.
Based on lot size, choose sample size code letter.
Based on sample size code and AQL, choose sample size and accept/reject numbers.

Example

Let us consider that we have received 1,000 solar PV modules from a supplier and we want to determine a sampling plan for inspection of microcracks using a go/no-go gauge. What will be the sample size and acceptance number if AQL is 1% for General Inspection Level II?

Using Table 1, the sample size code letter corresponding to General Inspection Level II and Lot Size range of 501 to 1,200 (for lot size of 1,000 as stated) is “J.” Now, in Table 2, referring to sample size code letter “J,” we get the prescribed number of samples, which is 80. From the same Table 2, for AQL of 1% and sample size as 80, we get the Acceptance number (Ac) = 2, and the Rejection number (Re) = 3. This implies that if two or fewer defects are found in the sample, accept the lot. Similarly, if the number of defects is three or more, reject the lot.

Conclusion

A good sampling plan is necessary for inspection at the lowest cost that will provide the best representation for the entire lot. ISO 2859 has proved to be the most vital standard toward selecting a good sampling plan. It is the most sought technical standard being used in the solar PV industry for sample size selection.

As evidence, we have three General Inspection Levels, that is, Level I, Level II, and Level III, and four Special Inspection Levels (S-1, S-2, S-3, and S-4). By default, General Inspection Level II should be used while using normal inspection. Similarly, Special Inspection Levels should be used when inspection time required per unit is larger, or whenever some destructive testing needs to be performed on sampled units.

The sampling methodologies and procedures described in this article are equally useful for power applications outside of solar PV. Sampling can be used on wind farm, gas turbine, and other power plant components. However, to facilitate the ease for sample selection in the solar industry, this article illustrates a detailed approach based on expertise and comprehensive analysis in that sector.

The sampling methodology, as described in this article, may be used in various applications in solar power plants. One of the applications is sampling of solar modules, as previously mentioned, to ascertain plant performance. Moreover, the detailed approach discussed in this article may be used effectively in both construction and operational phases of a solar power plant.

The same methodology was adapted for module testing at various solar plants, and the observed results were found to be very closely matched with desired plant performance. However, individual plant results may vary on a case-to-case basis.

—Satish Pandey is head of Analytics and Advisory, and Sumit Kumar is a senior engineer, both with Mahindra Teqo Pvt. Ltd.

Disclaimer: The information provided here is for general purposes and is offered in good faith. It is accurate to the best of our knowledge. Mahindra Teqo Pvt. Ltd. has not authenticated or validated the information provided, and assumes no responsibility or liability to any party or any person for the consequences of the use of the information contained herein.