A Proposed Definition of CHP Efficiency

Many alternative approaches for determining a useful definition of combined heat and power fossil power plant efficiency have been proposed, although most fail to produce a universal definition. This follow-up report to our February story on plant efficiency shows how an exergy analysis supplies the elusive solution.

Combined heat and power (CHP), also known as cogeneration, describes fossil-fired power plants that generate multiple product streams, usually thermal energy and electricity. In most cases, the thermal energy product comprises one or more streams of steam at different pressures and temperatures that are used by an end-use customer for district heating and/or cooling, manufacturing process needs, or similar industrial and/or residential uses.

The key benefit of CHP is the attractive economics produced by generating electricity and useful thermal energy from a single fuel source. A quick and easy assessment of the benefits of CHP can be found in “CHP: Helping to Promote Sustainable Energy” (POWER, June 2009).

Although there is no question about the benefit of CHP’s effectiveness in fuel utilization and reduced emissions, what has been missing so far is a standardized and consistent definition of CHP efficiency that would enable industry participants to measure and rank a wide variety of cogeneration plants on a thermodynamically consistent basis. This issue was recently discussed in “Plant Efficiency: Begin with the Right Definitions” (POWER, Feb. 2010), which pointed to the fundamental error of mixing “electricity apples with thermal energy oranges.”

A Rational Explanation

The second law of thermodynamics provides an unassailable measure of each product stream of a fossil-fired power plant: exergy, also called availability.

For the electric power product from a power plant, by definition, the exergy is exactly equal to the power generated. As dictated by one of the two fundamental corollaries of the second law, the Kelvin-Planck statement, the maximum useful work generating potential of any material stream is exactly equal to its thermodynamic property exergy.

For example, the most common material stream that is a product of CHP power plants is steam or hot water at a known pressure and temperature. Using steam tables, the exergy of steam or hot water can be exactly calculated. The numerical value that is obtained is exactly equal to the power that can be generated in a Carnot engine, which utilizes that particular product stream as its heat source. According to the second law, the Carnot engine is the most efficient energy conversion device possible when operating under a given set of temperature conditions.

A simple numerical example illustrates the calculation process using data taken from the steam tables. Suppose that a combined-cycle (CC) power plant supplies an industrial customer with 25,000 pph of saturated steam at 125 psia. The enthalpy of the steam is 1,191.1 Btu/lb for a total thermal energy supply of 29.8 million Btu/h (or 8,725 kWth). The exergy of 125 psia (saturated) steam is 369.9 Btu/lb for a total thermal exergy supply of 9.25 million Btu/h or 2,710 kWth. In other words, a hypothetical Carnot engine utilizing 29.8 million Btu/h of saturated steam at 125 psia as its sole heat source, and rejecting heat to the ambient at To (59F) would generate 2,710 kW of power, which implies a maximum theoretical thermal efficiency of 31.1%. Note that these two numbers—2,710 kW and 31.1%—are not subject to any misinterpretation because they are directly derived from a fundamental law of nature. Figure 1 shows the calculated results for a range of steam pressures and temperatures in terms of β, which is the ratio of steam exergy to steam energy (that is, enthalpy).

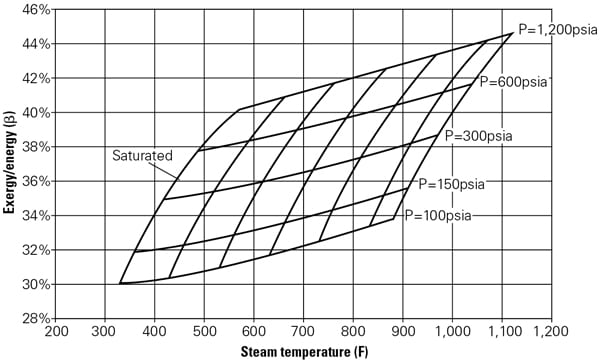1. Ratio of steam exergy to energy (enthalpy) for a range of steam pressures and temperatures. Exergy is given by e = (h – ho) – To · (s – so) where h is enthalpy, s is entropy, and both can be found from steam tables using p and T. The subscript denotes the reference “dead” state, which for this calculation is the ISO definition of po = 14.7 psia and To = 59F. Source: GE Energy

Obviously, it is practically impossible to design a Carnot engine. The state-of-the-art power plant engineering option available to a designer today is a steam turbine (ST). For illustrative purposes, consider what is practically possible with a ST with 85% isentropic efficiency discharging to a condenser at a pressure of 2.5 inches of mercury. Using 29.8 million Btu/h of saturated steam at 125 psia, this ST would generate 1,840 kW of shaft power for a thermal efficiency of only 21.1%. Though this seems to be a paltry number, consider that, when compared to the theoretically possible maximum of 2,710 kW (only from a hypothetical Carnot engine), the second-law or “rational” efficiency of the example steam turbine is 21.1%/31.1% = 67.9%. The term “rational” conveys the underlying concept of using a reference point that is theoretically possible instead of using a reference point that is (even theoretically) impossible.

Define the Calculation Process

The concepts of exergy and rational efficiency point to a thermodynamically consistent and unassailable evaluation of the efficiency of a fossil-fired CHP plant. The exact configuration of the power plant (simple-cycle gas turbine [GT] or CC power plant, fossil-fired ST power plant, integrated gasification CC power plant, or other), the type of fuel burned (natural gas, coal, or distillate), and the nature of product streams (such as steam, hot water, nitrogen, oxygen, or hydrogen) are absolutely immaterial. The proposed CHP efficiency can now be expressed as a simple formulation, in equation [1]:

where P is the net electric power generated by the prime movers in the plant; F is the total fuel consumed by the boilers, GT combustors, and similar combustion equipment in the plant on a net or gross basis, that is lower heating value (LHV) or higher heating value (HHV); and Ei is the exergy of the individual product streams i, where there are N of them in the particular plant.

Note that, as explained earlier, Ei is the maximum theoretically possible work that can be generated by a Carnot engine. The term εi in equation [1] is the second-law or rational efficiency of a practical engine (such as a steam turbine) that can reasonably be expected to convert theoretical Ei into actual electric power. Note that [1] can be rewritten in terms of Qi by using the exergy-to-energy ratio β, as shown in this restatement of [1]:

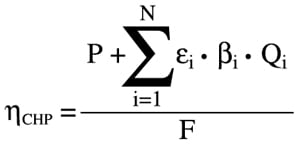
A conceptual graphical description of the ideas encompassed by [1] is shown in Figure 2. The CC power plant depicted in Figure 2 has two real products: electric power, P, and useful thermal energy, Q. There are two hypothetical products, which provide a measure of the quality of useful thermal energy, Q, via the second law of thermodynamics: thermal exergy E, which is the power that can be produced by a hypothetical and impossible Carnot engine, and the electric power equivalent of Q, P, which can be produced by a hypothetical and possible steam turbine, ST. Note that P and E are related to each other by the rational (second-law) efficiency of the steam turbine, ST, ε.

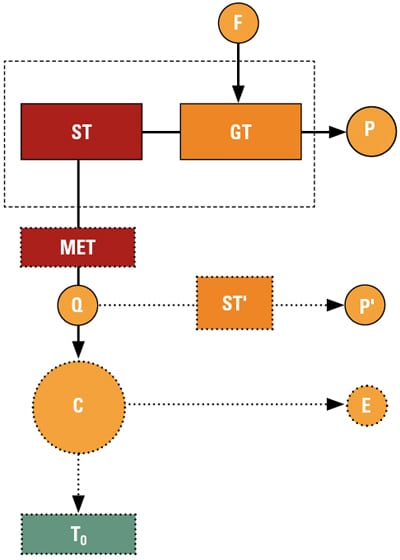2. Conceptual description of a CHP plant for a rational evaluation of plant efficiency via the second law of thermodynamics. F represents the fuel supplied to the combustion turbine and P is the net power produced by the combined cycle. The mean effective temperature (MET) determines the plant’s total thermal energy output, Q, and ST’ represents the hypothetical steam turbine that uses Q to produce net power P’. C represents the hypothetical Carnot engine that produces E, the plant’s total thermal exergy output. The Carnot engine operates between MET and a defined ambient temperature, To. Source: GE Energy

Because the most common cogeneration product is steam, the discussion below will focus on that.

Thermal energy and exergy, Q and E, respectively, are fixed by the pressure and temperature of the product stream. The exit or condensing conditions of the steam turbine, ST, are next selected. Please note that this is the only instance where an assumption is required to define the CHP efficiency given by [1]. An isentropic efficiency of 85% and a condenser vacuum of 1.25 psi (roughly 2.5 inches of mercury) can adequately represent today’s ST technology. Using the stated efficiency and condenser vacuum, ST rational efficiency can be calculated for a range of inlet steam pressures and temperatures (Figure 3).

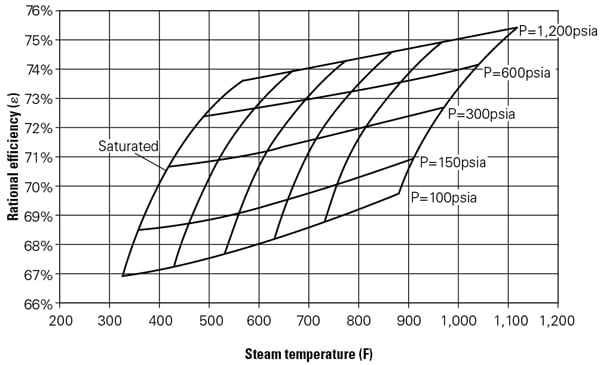3. The rational or second-law efficiency, ε, of a steam turbine as a function of throttle conditions. The steam turbine is assumed to have an isentropic efficiency of 85% and discharges to a condenser vacuum of 1.25 psi (about 2.5 inches of mercury) for a range of inlet steam pressures and temperatures. Source: GE Energy

Equation [1], along with steam tables and the rational efficiency from the chart in Figure 3, constitute an internally consistent and thermodynamically meaningful framework for the evaluation of the efficiency of CHP plants. If the chart in Figure 3 seems too unwieldy for practical applications, the concept of mean-effective temperature (MET) can be used for an alternate and more elegant approach. In fact, MET is a parameter that has the units of temperature in degrees Fahrenheit and is equivalent to exergy in terms of measuring the quality (the useful work generation potential) of a material stream at a given pressure and temperature (and composition for gaseous streams). In conceptual terms, it is the constant temperature of the hypothetical hot temperature reservoir of the hypothetical Carnot engine, which receives heat, Q, at MET and rejects heat to a low-temperature reservoir at To to generate useful work, E. Thus, MET is a single figure-of-merit that contains all the information provided by P, T, Q and E, as shown in equation [2]:

When the information contained in Figure 3 is recast in terms of MET using [2], in which β = E/Q, the result is a simple curve, which is depicted in Figure 4. The rational efficiency found from Figure 4 is universally valid when comparing the efficiency of any combined heat or standard steam power plant.

4. The rational or second-law efficiency, ε, of a steam turbine as a function of mean-effective temperature (MET). The steam turbine is assumed to discharge to a condenser vacuum of 1.25 psi (about 2.5 inches of mercury) with an isentropic efficiency between 80% and 85%. The horizontal axis is the mean effective temperature of the inlet steam at pressures and temperatures in Figure 2. Source: GE Energy

An Example Clarifies the Concepts

The advantage of the proposed CHP plant rational efficiency is best demonstrated by using a simple numerical example. Consider a 1 x 1 CC power plant based on an E-Class GT and condensing ST. Three variants of this CC plant, one for electric power generation and two for cogeneration applications, are summarized in Table 1. Note that the numbers in Table 1 are for illustrative purposes only and do not reflect an existing or commercially offered product.

Table 1. ISO baseload performances of three combined-cycle power plant variants (1 x 1 with an E-Class GT). Plant A is for electric power generation only and has a net electric power output of 130 MW. Plant B is a combined-cycle combined heat and power (CC CHP) plant that provides saturated steam at 125 psia to an industrial customer. Plant C is also a CC CHP plant that provides superheated steam at 1,200 psia and 800F to an industrial customer. Note that, in terms of total useful thermal energy supply to the customer, Plants B and C are equivalent at 50 MWth. The total power production of Plants A and B reflects comparable ST technology after extracting the specified amount of steam from the bottoming cycle. Source: GE Energy

Plant A is clearly the most valuable variant from a thermal efficiency perspective from the options listed in Table 1. Furthermore, although both Plants B and C deliver the same amount of thermal energy, 50 MWth, Plant C is the more valuable variant because its steam product is of a much higher grade of energy. This is reflected by the calculated exergy and MET values of the process steam provided by Plants B and C.

As seen from the data in Table 2, all definitions are equivalent as far as Plant A is concerned, with the exception of thermal efficiency, which uses the gross heating value (HHV) of the fuel as a basis. This is not surprising, because the only product of Plant A is electric power supplied to the grid. However, neither the thermal efficiency nor the PURPA (Public Utility Regulatory Policies Act) efficiency or heat chargeable to power (HCP) are able to provide a correct measure of the much higher grade of the steam product from Plant C vis-à-vis Plant B. All three conventional CHP efficiencies mistakenly assign the same value to the thermal energy products of Plants B and C. They do not make a distinction between different grades of steam. In other words, 100 psia (saturated) steam is implicitly considered as equivalent to 1,200 psia superheated steam at 800F (Plants B and C).

Furthermore, these CHP definitions evaluate Plants B and C, which are based on an E-Class GT, at an efficiency that is equivalent to an F-Class GT. This is an example of mismeasurement, which would be even more glaring in the presence of supplementary firing in the heat-recovery boiler. As can be seen in Tables 1 and 2, when Plant C is duct-fired to generate twice the amount of original process steam, two definitions return a CHP plant efficiency that is equivalent to or even better than an H or J-Class GT.

What should be emphasized is the fact that the conventional measures not only mix “electricity apples with thermal energy oranges,” but they also totally ignore the variation in quality among the “thermal energy oranges” themselves. One can certainly make the reasonable argument that “beauty is in the eye of the beholder.” In other words, an industrial customer that needs 125 psia (saturated) steam for his manufacturing plant is really not interested in the fact that 1,200 psia and 800F steam is thermodynamically more “valuable.” If Plant B fits his power and thermal energy needs, he will go with Plant B, which is more valuable for him, and that is that. This is an unavoidable fact of life when one has to evaluate the differences between products within the same category.

Subjective considerations, which can almost always be expressed in monetary terms, cannot be excluded when evaluating design options. However, this fact does not obviate the need for a scientifically objective means of evaluating different products on a common basis so that different designs can be compared and evaluated in a rational manner. Furthermore, such a rational method of measurement, especially when adopted by regulatory definitions and incentive programs, would drive the most efficient use of fuel and the lowest possible emissions while preventing inherently low-technology plants from “sneaking under the standard” by accounting tricks.

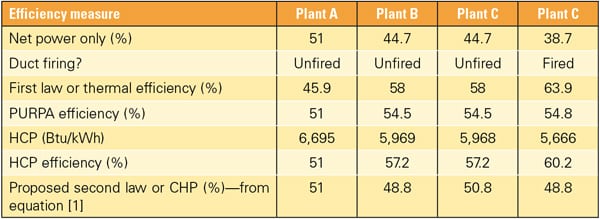Table 2.    CHP efficiencies for the CC cogeneration power plants described in Table 1 using different definitions. The thermal or first-law efficiency is calculated by adding the electricity production to the thermal energy production and dividing by the fuel supplied to the plant on a HHV basis. The PURPA efficiency is calculated in the same manner, but the thermal energy is weighted, by legislative definition, by a factor of one-half. The heat chargeable to power or HCP, in units of Btu/kWh, is the energy charged to net electric power after subtracting the amount of fuel that would be required to generate an equivalent amount of steam (thermal energy) in a conventional fired boiler with an assumed LHV efficiency of 90%. The HCP efficiency is found by dividing HCP into 3,412.12 Btu/kWh, a conversion factor. The origin or justification for factors such as one-half or 90% is unclear.

Table 2 shows how [1] does exactly that and ranks the three plants in a rational manner by putting Plant A in its rightful place at the top because it has the most valuable product, electricity. It should be recognized that if Plants B and C were designed by the same “perfect designer” with absolutely no consideration of size, materials, complexity, and cost, they would have exactly the same efficiency. Not only that, but their efficiency would be exactly the same as that of Plant A, 51%, if that plant were also designed by the same “perfect designer.” This is so because using a rational efficiency for the thermal energy product (steam) of both Plants B and C that would exactly reflect the same bottoming cycle configuration and technology as in Plant A, the value assigned to each thermal energy product would be exactly the same as the lost ST power generation due to the diversion of generated steam to the process customer.

Also note that the nearly two points of efficiency disadvantage of Plant B vis-à-vis Plant C per [1] is indicative of its less-advanced ST technology. This distinction is not obvious from the total electric power outputs or power-only efficiencies of these plants, which are numerically equivalent. This fact clearly illustrates the power of [1] as an objective and extremely reliable means of differentiating between myriad cogeneration plants with different technology levels and differing supplies of thermal energy.

–S. Can Gülen, PhD, PE (can.gulen @ge.com) is a principal engineer with GE Energy.