Drum pressure the key to managing boiler stored energy
At the heart of most boiler combustion control systems (and most coordinated boiler/turbine control systems as well) is throttle pressure correction, usually applied by the "master controller." Throttle pressure is considered a key variable to control because it represents the energy balance between the boiler and the turbine.
When throttle pressure is constant, the boiler is supplying the optimal amount of energy to the turbine. It is said that "the boiler is balanced with the turbine." Any prolonged deviation from setpoint will reduce efficiency. For example, at a lower throttle pressure, producing the same amount of electrical energy would require increased steam flow and thus an increased boiler firing rate.
However, because of process latencies, nonlinearities, and interaction, a control system that uses throttle pressure as its primary controlled variable will produce instability and oscillation. Stable operation can be achieved only by restricting the rate and magnitude of load changes.
To overcome the instabilities and allow for faster load changes, "feed-forward" signals—typically based on boiler steam flow or turbine first-stage pressure—are commonly added to the system. The feed-forwards may or may not include intelligence to deal with nonlinear response. However, most steam flow feed-forwards are "regenerative" in nature. That is, they tend to produce negative interaction with the pressure control as a result of disturbances in the boiler or, more importantly, when the heating value of the fuel changes. When the fuel’s heating value changes, the feed-forward will produce a response to compensate for the change, but with an opposite (incorrect) polarity, thus creating further instability. As a result, feed-forwards tend to be detuned, and their use with solid fuel–fired boilers is quite limited. Figure 1 shows such a system.
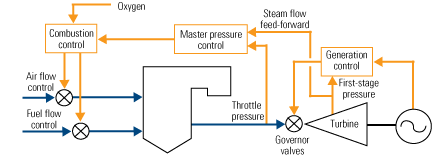
1. Asking for trouble. Here is a simple master pressure control with a steam flow feed-forward signal based on turbine first-stage pressure. Because the feed-forward is regenerative, it will respond incorrectly to boiler disturbances and changes in fuel heating value. Unless intelligent compensation is provided, the feed-forward signals will "fight" with the pressure correction imposed by the master controller, which relies on integral action during load changes. Source: Metso Automation
Time delays and nonlinear responses must be addressed by the control system designer. For example, a boiler’s "time constant"—the time it takes its output to reflect two-thirds of the impact of an input change—can be several minutes in duration. Even with the aid of a well-tuned feed-forward, any increase in load will produce a pressure drop that can cause instability and cycling due to excess integral action by the master pressure control. Realize that most generation control systems are designed to modulate the turbine governor valves to provide maximum linear response to the new load target. Accordingly, when load increases, the system opens the valves to extract more stored energy (in the form of increased steam flow) to meet demand. But it may take as long as 2 minutes before pressure returns to the setpoint level, and during this period pressure may overshoot and break into oscillation.
The long delay is due in part to the fuel delivery system and to the boiler’s heat-transfer characteristics. Throttle pressure will lag and continue to fall during the load increase, causing severe controller "windup." When pressure begins to increase, the master controller will integrate in the opposite direction, introducing another lag, which again may lead to cycling. To overcome this problem, it is recommended that the integral action be set to a relatively small value (usually much less than 1).
A well-designed pressure correction algorithm typically comprises a compensated feed-forward (proportional control) and largely derivative action. A well-tuned control system should be able to stabilize pressure within two boiler time constants. Unfortunately, too many pressure control systems still rely on integrating master pressure controls and less-than-optimum feed-forwards. Even coordinated control systems that utilize a common unit demand do not do justice to the problem. Unit demand, though not necessarily regenerative, does not usually include the intelligence to deal adequately with the delays and boiler stored-energy issues.
Control strategies: Still imperfect
For more than four decades, control system designers have struggled to develop strategies for simultaneously controlling the turbine and boiler, balancing generation and system demand, balancing the boiler with the turbine under all conditions, and protecting the unit from mismatches or unsafe conditions. Current conventional wisdom assumes that coordinated boiler/turbine control strategies apply a common unit demand directly and simultaneously to the control systems of the boiler and the turbine governor.
In theory, because generation control and boiler control derive their setpoints from the same set of requirements, and operate in parallel in the same time domain, they should work in concert to maximize unit response. Performance characteristics and response limitations of both the turbine and the boiler are included in the demand calculation.
Coordinated boiler turbine control was first implemented in the late 1950s by Leeds & Northrup Co. on the first set of supercritical-pressure and -temperature units built in the U.S. This system, executing the so-called Direct Energy Balance, or D-E-B, strategy, has been modified and updated over the years to make it more responsive, especially when used on large coal-fired units. Figure 2 shows the general characteristics of a typical, present-day coordinated control strategy.

2. Linear, within limits. A typical coordinated control strategy imposes a common unit demand on the turbine and boiler. The generation control is designed to linearize and speed megawatt response and to make maximum use of boiler stored energy. The boiler control depends on the application of dynamic rate action to firing rate demand to compensate for boiler stored energy. The dynamic rate is typically applied linearly with respect to load, so it does not compensate for nonlinearities (with respect to load) in stored energy. During load changes, the integral action is typically disabled to prevent "windup" and instability. Source: Metso Automation
Generation control is typically based on megawatts, turbine first-stage pressure, and/or frequency. Using these simple variables, it is possible to produce linear generation response, allowing the unit to participate in remote dispatching (automatic generation control, or AGC) and load frequency control. This form of generation control makes maximum use of boiler stored energy to change electrical load at the maximum rate permitted by the boiler and its auxiliaries. But when the generation control is withdrawing stored energy to meet unit demand at the maximum rate, throttle pressure will decay rapidly. The master controller must recognize and compute the stored energy requirements and control the combustion rate to meet those requirements. Because it must do so without causing instability and cycling, it must minimize the use of integral control.
Management and use of stored energy is the key to maximizing rate of change, and the boiler control strategy must provide a means for doing both. Specifically, it must control the firing rate precisely to accommodate the boiler’s stored energy requirements, and to do that the control strategy must be able to infer the real heat release in the furnace.
To summarize, the strategy must include:
- A nonregenerative feed-forward that does not respond to boiler upsets or changes in fuel quality.
- A means to control pressure with minimal use of integral control.
- A computation of the change in stored energy (as opposed to its absolute value), based on the true heat release in the furnace.
- A means to limit the unit’s rate of change of combustion in the event that the boiler or its auxiliaries cannot support the new rate.
Boiler stored energy
Stored energy is a function of the enthalpy of the steam/water mixture in the boiler’s water walls and surrounding metal. Both are significant, and vary nonlinearly with steaming rate and boiler pressure (because the density of both steam and water increases nonlinearly with increases in pressure). As pressure increases, more steam and water can be contained in the same volume, increasing the enthalpy of the mixture and the stored energy in the boiler. As load increases, the change in stored energy must be supported by overfiring, in addition to that required to support the new output level. Boiler demand must be adjusted to compensate for this incremental energy.
Figure 2 shows the application of "dynamic rate" to add overfiring during a load increase. The rate applied is a function of load, but for the most part it is an arbitrary function and not derived from the true heat release. Figure 3 shows dynamic rate applied to a load demand increase (the broken blue line). No attempt is made to compute the new requirement for stored energy; the actual overfiring requirement will most likely track the broken red line. A means must be found to compute this value and apply it to the boiler firing rate demand. The solution lies both in the response of the turbine governor valves and in drum pressure measurement. Let’s now show how a boiler model can be used to develop a control solution.
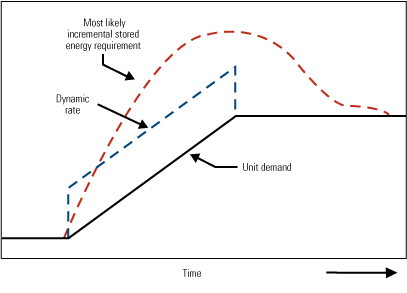
3. Close, but no cigar. This chart shows the effect of using dynamic rate compensation to overfire a boiler to compensate for unit demand during a load increase. The strategy provides for an incremental change in boiler stored energy, but because the level is typically arbitrary, this is a compromise solution. The actual stored energy requirement, which tracks the broken red line, is not easily predetermined. The control strategy must include a method for self-calibrating the level of actual incremental over-firing at all loads. Source: Metso Automation
Basing control on Heat Release
It is well known that in a steam plant, the energy output of the boiler (its main steam flow) is proportional to its energy input. But that is only true under steady-state conditions. A more accurate relationship between the boiler’s energy input and output must also account for changes in its stored energy.
It’s much more important to measure the change in a boiler’s stored energy (caused by a change in its firing rate or the heating value of its fuel) than to measure the absolute value of that energy. Control systems designers do so by modeling the entire process, as shown in Figure 4, from the fuel delivery system to the generator.
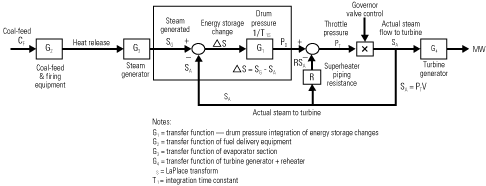
4. Drum boiler model. This simple control model would be capable of computing the level of incremental stored energy in a drum-type boiler. The drum integrates the difference between energy in and energy out (main steam flow). Under steady-state conditions, this difference is zero. Source: Metso Automation
In a drum-type boiler, most of the working medium (water and steam) is at saturation pressure and temperature. As load increases, so does drum pressure (PD), increasing the saturation temperature and steam enthalpy in the process. Because drum pressure has a linear relationship with fluid enthalpy, it is a good index of stored energy. As load increases, the metal temperatures of the boiler’s water walls also increase and retain significant amounts of heat; the heat retained by the fluid and metal can be considered collectively as one heat capacitance. It’s worth noting from Figure 4 that the pressure drop across the superheaters (RSA) is a nonlinear function of load.
Earlier, we mentioned that the boiler’s energy input is proportional to its energy output, plus or minus the change in its stored energy. In the center of Figure 4 is the key term ΔS, which represents the change in stored energy—exactly what we need for our energy input calculation. ΔS = SG x2013; SA, where SG is steam generated and SA is the steam actually sent to the turbine. Accordingly, within any measurement of SG is a measurement of the heating value of the boiler’s fuel input, independent of any change in boiler stored energy (ΔS). Although this value cannot be measured directly, it can be derived from measurements of steam flow and drum pressure.
The equation also can be written as: dS/dt = dSG/dt – dSA/dt
Under steady-state conditions, dS/dt is zero, because all of the steam generated flows to the turbine. If, however, the steam to the turbine (SA) is greater or less than the steam generated (SG), drum pressure will fall or rise to reflect the withdrawal or addition of stored energy.
The boiler integrates the difference between the steam generated and the steam delivered to the turbine. Note that in Figure 4, the transfer function for G1 is an integrator. Accordingly, the rate of change of drum pressure (dPD/dt) is a legitimate variable from which to infer stored energy changes, because the integral of dPD/dt is PD.
The actual steam flow to the turbine (SA) is a function of the aggregate governor valve position. However, we use turbine first-stage pressure (P1) rather than main steam flow because the former can be measured simply and accurately. As an excellent indicator of turbine energy flow, it is used as one of the process variables in the development of the firing rate demand to the boiler. If needed, steam flow can be calculated from P1 by temperature compensation.
Thus, the equation for heat release can be written: Heat release = KP1 + K1(dPD/dt)
Figure 5 represents the boxed-in portion of Figure 4 where heat release is derived.
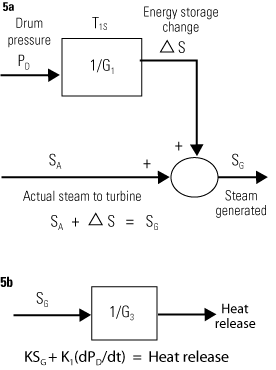
5. Computing heat release. Figures 5a (for steam generated) and 5b (for Heat Release) are derivations that represent the boxed-in part of Figure 4. Steam generated (SG) is actual steam (SA) plus or minus the changed in stored energy (S). In Figure 4, the "G" transfer functions are integrals, but in 5a the transfer function 1/G1 (from drum pressure, PD) is a derivative. At steady state, when drum pressure is constant, its derivative is zero and the steam generated is equal to the actual steam flow. Turbine first-stage pressure (P1) is frequently substituted for steam flow and is used here in our calculation of heat release. Source: Metso Automation
Using drum pressure for control
A key part of the heat release concept is the realization that the derivative of drum pressure, like the integral of throttle pressure error, is indicative of boiler-turbine balance and thus can be used to effectively measure and control fuel input. Calculating and using Heat Release (as the software will be called) as the fuel feedback eliminates reliance on integral control and minimizes system instability and cycling. Instead of using master pressure control in our boiler control strategy, we will instead rely on calculations of turbine energy that are, in themselves, self-calibrating with respect to firing rate (and including changes in stored energy).
Figure 6 shows the boiler model with the new strategy—a simple example of combustion control using parallel control of fuel and air. Note that heat release is the fuel feedback, and that the fuel control system does not use total coal feeder speed. Heat release provides a real-time indication of energy input to the boiler that is sensitive to changes in heating value and remains accurate even if coal firing is supplemented by co-firing of oil or gas. Heat Release inherently provides a total fuel computation.
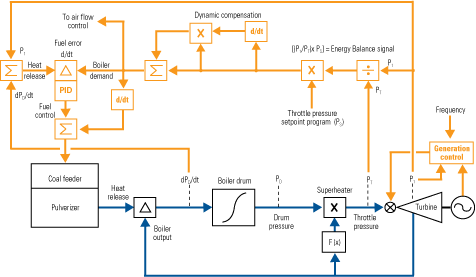
6. Balanced approach. A simplified boiler model with Direct Energy Balance (D-E-B) control. D-E-B employs proportional and derivative action and excludes integral action, thus ensuring stable control during load changes. The self-calibrating energy demand computation—the Energy Balance signal—adjusts boiler demand for the correct incremental stored energy requirement during a load change. The heat release computation is correct for multiple fuel firing and senses changes in fuel heating value in real time. The generation control is a three-element cascade loop that linearizes the governor valve’s action in response to load and provides for frequency control. Source: Metso Automation
Firing rate demand is a self-calibrating turbine energy calculation based on the ratio of turbine first-stage pressure to throttle pressure. Called the Energy Balance signal, it responds only to changes in aggregate valve position reflecting turbine energy demand. The signal is nonregenerative (it is not affected by disturbances in the boiler or changes in fuel quality) but must be compensated by throttle pressure setpoint if the unit is operated at less than design pressure. For example, if the unit were to be operated in sliding-pressure mode at 70% of rated pressure, the Energy Balance signal would be multiplied by 0.70.
As electrical load is increased in Figure 3, the Energy Balance signal would follow the broken line. It will overfire the boiler as needed to meet the new load point and the incremental change in stored energy. Note that dynamic compensation is still applied, but now with minimal action. Dynamic rate calculations are linear and/or a function of load, but they do not accurately portray the correct relationship of load versus the change in stored energy.
D-E-B lives on
Direct Energy Balance coordinated control is based on the principles described above and notably includes:
- The Energy Balance signal—a self- calibrating proxy for firing rate demand that is based on turbine energy.
- Pressure correction—dependent on derivative action only.
- Heat Release—a real-time calculation that accounts for all fuel entering the boiler, its energy output, and its change in stored energy.
- Drum pressure—the key variable in the current generation of D-E-B coordinated control systems. Its derivative is used as an indicator of incremental stored energy and for pressure correction—without introducing instability.
Figures 7, 8, and 9 show some key data from a 660-MW coal-fired unit that uses Metso Automation’s version of the D-E-B control system under the umbrella of a maxDNA automation system.
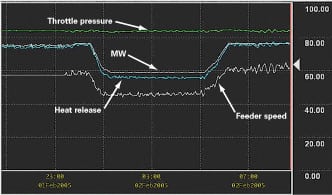
7. Steady as she goes. In this test response of the D-E-B control system on a 660-MW coal-fired drum-type boiler, heat release, rather than feeder speed, is used as the fuel feedback. Source: Metso Automation
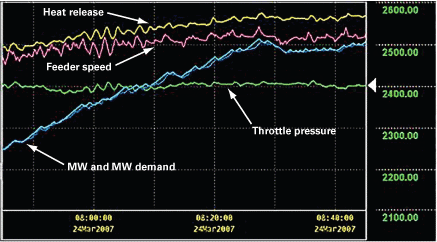
8. Better AGC stability. With the same 660-MW unit operating in automatic generation control mode, note that the MW and unit demand curves are virtually identical. Source: Metso Automation
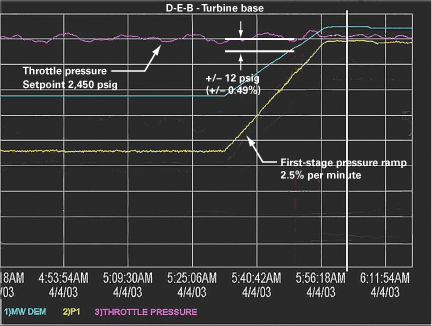
9. Follow the leader. The unit’s load ramp in D-E-B coordinated mode. Note the linear response of the boiler output (turbine first-stage pressure). Source: Metso Automation
Recently, the generic version of Metso’s system was upgraded with:
- A means to recalibrate the Heat Release computation on-line if feedwater temperature were to change (for example, if a feedwater heater were to become less efficient or be removed from service).
- A means to reduce the unit’s rate of load change as key process variables approach unacceptable levels and to stop it when those variables exceed safe levels.
—Roger A. Leimbach is Metso Automation’s director of applications and marketing. He can be reached at [email protected].